3. ΣΥΜΜΕΤΡΙΕΣ ΣΥΝΑΡΤΗΣΗΣ

    Για να έχουμε μία συμμετρική γραφική παράσταση Cf ως προς άξονα y΄y είτε ως προς κέντρο Ο(0,0), θα πρέπει να έχουμε Πεδίο Ορισμού D_f συμμετρικό ως προς το 0.
Δηλαδή: Για κάθε x ∈ D_f , θα πρέπει -x ∈ D_f.
    Μία συνάρτηση λέγεται άρτια αν για κάθε x ∈ D_f , ισχύει f(-x) = f(x). Μία άρτια συνάρτηση είναι συμμετρική ως προς τον άξονα y΄y.
    Μία συνάρτηση λέγεται περιττή αν για κάθε x ∈ D_f , ισχύει f(-x) = -f(x). Μία περιττή συνάρτηση είναι συμμετρική ως προς την αρχή των αξόνων.

    Διατρέχουμε τα σημεία της γραφικής παράστασης της συνάρτησης και θεωρούμε κάθε φορά το x, το -x, το f(x) και το f(-x). Αν για όλες τις τιμές του x, οι τιμές των f(-x) και f(x) είναι ίσες, η συνάρτηση είναι άρτια,ενώ αν οι τιμές των f(-x) και f(x) είναι αντίθετες, η συνάρτηση είναι περιττή.

Θεωρούμε τη συνάρτηση f (x) = 2x^3 :

f[x_] := 2x^3

    Σχεδιάζουμε τη γραφική παράσταση σημείων της συνάρτησης σ’ ένα καρτεσιανό σύστημα συντεταγμένων:

k = Plot[f[x], {x, -2, 2}, PlotStyle→ {RGBColor[0, 1, 0], Thickness[0.015]}, AspectRatio->1, PlotRange-> {{-2.5, 2.5}, {-20, 20}}]

[Graphics:../HTMLFiles/A Lyceum, Studying functions_91.gif]

-Graphics -

    Διατρέχουμε τα σημεία της γραφικής παράστασης της συνάρτησης και θεωρούμε κάθε φορά το x, το -x, το f(x) και το f(-x):

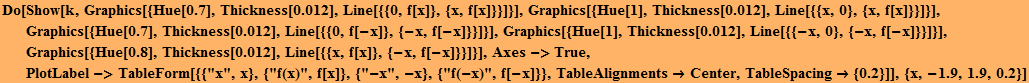
[Graphics:../HTMLFiles/A Lyceum, Studying functions_114.gif]

    Θεωρούμε τον πίνακα τιμών της συνάρτησης:  

TableForm[Table[{x, f[x]}, {x, -2, 2, 0.5}], TableHeadings→ {None, {"x", "f(x)"}}, TableAlignments→Center, TableDirections->Row]

x -2 -1.5 -1. -0.5 0. 0.5 1. 1.5 2.
f(x) -16 -6.75 -2. -0.25 0. 0.25 2. 6.75 16.

    Τι συμπεράσματα μπορούμε να βγάλουμε για τις συμμετρίες της y = f(x);




Θεωρούμε τη συνάρτηση g (x) = 2x^4 :

g[x_] := 2x^4

    Σχεδιάζουμε τη γραφική παράσταση σημείων της συνάρτησης σ’ ένα καρτεσιανό σύστημα συντεταγμένων:

m = Plot[g[x], {x, -2.1, 2.1}, PlotStyle→ {RGBColor[0, 1, 0], Thickness[0.015]}, AspectRatio->1, PlotRange-> {{-2.5, 2.5}, {-4, 34}}, DefaultFont→ {"Times", 15}]

[Graphics:../HTMLFiles/A Lyceum, Studying functions_119.gif]

-Graphics -

    Διατρέχουμε τα σημεία της γραφικής παράστασης της συνάρτησης και θεωρούμε κάθε φορά το x, το -x, το g(x) και το g(-x):

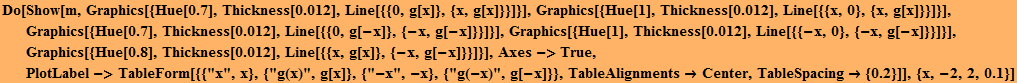
[Graphics:../HTMLFiles/A Lyceum, Studying functions_163.gif]

    Θεωρούμε τον πίνακα τιμών της συνάρτησης:  

TableForm[Table[{x, g[x]}, {x, -2, 2, 0.5}], TableHeadings→ {None, {"x", "g(x)"}}, TableAlignments→Center, TableDirections->Row]

x -2 -1.5 -1. -0.5 0. 0.5 1. 1.5 2.
g(x) 32 10.125 2. 0.125 0. 0.125 2. 10.125 32.

    Τι συμπεράσματα μπορούμε να βγάλουμε για τις συμμετρίες της y = g(x);





Created by Mathematica  (November 4, 2015) Valid XHTML 1.1!